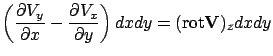: Refelction and Transmission
: Maxwell Equation
: Wave Equations
Now we think a interface which is the boundary medium 1 and 2 as shown in Fig.1.
From Gauss law, we can get the following for the Gauss box
which include the interface inside the box,
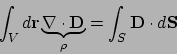 |
(38) |
In the limit that the Gauss box is very thin
![\begin{displaymath}
\int_V d{\bf r} \rho =Q_{\rm box} =
{\bf n} \cdot [ {\bf D}_1 - {\bf D}_2 ] S
\end{displaymath}](img101.png) |
(39) |
where vector 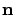 means the unit vector pointing from media 1 to 2.
means the unit vector pointing from media 1 to 2.
![\begin{displaymath}
{\bf n} \cdot [ {\bf D}_1 - {\bf D}_2 ] = Q_{\rm box}/S
= \sigma_{12}
\end{displaymath}](img103.png) |
(40) |
From
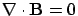
![\begin{displaymath}
{\bf n} \cdot [ {\bf B}_1 - {\bf B}_2 ] = 0
\end{displaymath}](img105.png) |
(41) |
Stokes theorem:
In Fig.1.3
�$B?^�(B 1:
Gauss and Stokes box
|
|
�$B?^�(B 2:
Stokes theorem
|
|
From Eq.3
From Eq.4



: Refelction and Transmission
: Maxwell Equation
: Wave Equations
Yamamoto Masahiro
�$BJ?@.�(B14�$BG/�(B8�$B7n�(B30�$BF|�(B
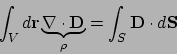
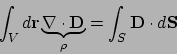
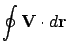
![$\displaystyle V_x (x_0, y_0 )dx + [V_y (x_0, y_0 ) + \frac{\partial V_y}{\partial x}dx ]dy$](img109.png)
![$\displaystyle - [V_x (x_0, y_0 ) + \frac{\partial V_x}{\partial y}dy ]dx -
V_y (x_0, y_0 )dy$](img110.png)