


: Brewster angle
: Reflection and Transmission Coefficients
: Reflection and Transmission Coefficients
In usual we asuume that
![$\sigma_{12}(k\sin\theta, \omega)=0, {\rm Im}\tilde{n}=0, \mu_1 = \mu_2 =1,
\le...
...sin\theta, \omega) \right]_x = 0,
\left[J_s (k\sin\theta, \omega) \right]_x = 0$](img233.png) , then
for p-wave
, then
for p-wave
and for s-wave
If we define
and for s-wave
And we finally get
The reflectance 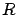 is defined as the ratio of the reflected power (or flux) to
the incident power
is defined as the ratio of the reflected power (or flux) to
the incident power
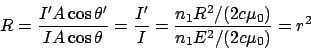 |
(112) |
The radant flux density 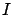 is given by the averaged
Poynting vector
is given by the averaged
Poynting vector
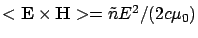 In the same way The transmittance T may be
In the same way The transmittance T may be
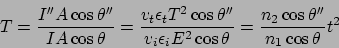 |
(113) |
�$B?^�(B 4:
He-Ne laser from air to water
![\includegraphics[width=8cm]{air2water_reftrans.eps}](img263.png)
![\includegraphics[width=8cm]{air2water_reftrans2.eps}](img264.png) |
�$B?^�(B 5:
He-Ne laser from water to air
![\includegraphics[width=8cm]{water2air_reftrans.eps}](img265.png)
![\includegraphics[width=8cm]{water2air_reftrans2.eps}](img266.png) |



: Brewster angle
: Reflection and Transmission Coefficients
: Reflection and Transmission Coefficients
Yamamoto Masahiro
�$BJ?@.�(B14�$BG/�(B8�$B7n�(B30�$BF|�(B
![]() , then
for p-wave
, then
for p-wave
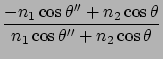
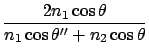
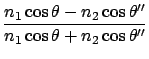
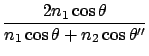
![]() is defined as the ratio of the reflected power (or flux) to
the incident power
is defined as the ratio of the reflected power (or flux) to
the incident power